Newton Raphson’s Method in Python

In this tutorial we will explore the Newton Raphson’s Method in Python. Newton’s method is a special mathematical technique we can use the locate the Root of a Equation. The process can get a little tedious to do by hand, as it involves many iterations. Luckily, we can easily make a code implementation for it, which will be the focus of today’s tutorial.

Code Explanation

To get access to some special mathematical operations, we will be using the SymPy Library for Scientific Computation.

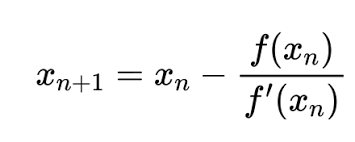
Shown above is the formula for Newton’s Method. To briefly sum up how it works, it starts out with an initial value of “x”, and continuously updates this value over a series of iterations. After a certain number of iterations, the value of “x” converges to the Root.

from sympy import symbols, diff
x = symbols("x")

First we need to import the diff (for differentiation) and the symbols function from SymPy. The symbols function is used to create unknowns, such as “x” and “y”. These act as actual variables into which we can later substitute values into.

f = x**2  - x - 6   
x0 = 0
n = 10

Here we create a bunch of variables to work with. “f” is an expressions, utilizing the variable “x” we created earlier. x0 is the initial value of x, and n is the number of iterations.

for i in range(n):
    x0 = x0 - float(f.subs(x, x0) / diff(f, x).subs(x, x0))
    print(x0)

Here is the main logic behind our code. We are iterating over the code “n” times, updating the value of “x” in every iteration. If you are having trouble understanding any of the code in this part, refer to formula from earlier.

Code for Newton Raphson’s Method

The complete python code + output for the Newton Raphson’s Method.

from sympy import symbols, diff
x = symbols("x")

f = x**2  - x - 6   
x0 = 0
n = 10

for i in range(n):
    x0 = x0 - float(f.subs(x, x0) / diff(f, x).subs(x, x0))
    print(x0)

print("Root: ", x0)

-6.0
-3.230769230769231
-2.203013481363997
-2.007623800972449
-2.0000115891269745
-2.0000000000268616
-2.0
-2.0
Root:  -2.0

Interested in other similar tutorials in Python? Check out our tutorial on Taylor Series!

This marks the end of the Newton Raphson’s Method in Python tutorial. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can be asked in the comments section below.