Differentiation and Integration with Python SymPy

Differentiation and Integration are an essentials component of many major mathermical operations and formulae. With Python SymPy, you can not only create and manipulate mathematical expressions, you can also perform differentiation and integration on them!

This tutorial will be mostly focused on differentiation and integration of Python SymPy expressions. For those new to SymPy, check out our SymPy Tutorial for Beginners to learn more!

Differentiation of Expressions in SymPy

To differentiate expressions in SymPy, we use the diff() method on SymPy expressions. Depending on the type of parameters passed in, it will return the differential of that expression.

The first parameter is the expression that you want to differentiate, and the second parameter is what you wish to derivative with respect to. e.g: “Derivate with respect to x” (shown in the below example).

from sympy import symbols, diff
x, y = symbols("x y")

expr = 5*x
print(diff(expr, x))

Let’s take a look at another example.

expr = x**2 - x - 6
print(diff(expr, x))

2*x - 1

If you wish to differentiate an expression multiple times, there are two ways of doing so. The first method is by simply including the symbol you wish to derivate with respect to, multiple times.

expr = x**4

print(diff(expr, x))
print(diff(expr, x, x))
print(diff(expr, x, x, x))

4*x**3
12*x**2
24*x

Don’t forget that these returned expressions are SymPy expressions on which we can use solve(), subs(), expand() and other similar functions.

Alternatively, you can include an integer “n” as a parameter after the symbol, and it will differentiate it “n” times.

expr = x**4

print(diff(expr, x, 1))
print(diff(expr, x, 2))
print(diff(expr, x, 3))

4*x**3
12*x**2
24*x

Furthermore, you can also differentiate with respect to multiple symbols within a single diff() function.

expr = y*x**2 + x*y**2
print(diff(expr, x, y))

2*(x + y)

There are two ways we can use diff(). Either as a function, or as a method. The output is the same either way; the only difference is the first parameter.

expr = x**2 - x - 6
print(expr.diff(x))

2*x - 1

Interested in seeing examples on how to differentiate and integrate trigonometric functions in SymPy? Check out our dedicated tutorial on Trigonometric Identities in SymPy.

Integration in Python SymPy

It’s time for Integration with SymPy. Let’s take a look at how we can integrate various mathematical expressions and obtain their integral forms.

Just like differentiation, we have a function for integration in SymPy called integrate(). It also takes the same parameters, which is the symbol by which we wish to integrate the expression by.

Let’s take a look at some examples.

from sympy import symbols, diff, integrate
x, y = symbols("x y")

expr = 2*x
print(integrate(expr, x))

x**2

It is important to note, that SymPy does not include the constant “c” when integrating.

A slightly more complex expression being integrated.

expr = x**2 - x - 6
print(integrate(expr, x))

x**3/3 - x**2/2 - 6*x

Here’s what happens when you integrate an expression with multiple symbols, with respect to just one of those symbols.

expr = x + y + 2
print(integrate(expr, x))

x**2/2 + x*(y + 2)

We can also integrate multiples times within a single function. This method involves simply passing the symbol repeatedly as a parameter. If you pass it in three times, it will integrate it thrice.

expr = 8*x

print(integrate(expr, x, x, x))

x**4/3

We can also integrate with respect to multiple symbols within a single function.

expr = x + y 
print(integrate(expr, x, y))

x**2*y/2 + x*y**2/2

The above equation looks a little hard to understand. Luckily, SymPy gives us the pretty_print function that we can use to display expressions in a more human-friendly way.

from sympy import symbols, diff, integrate, pretty_print
x, y = symbols("x y")

expr = x + y 
print(pretty_print(integrate(expr, x, y)))

 2         2
x ⋅ y   x ⋅y
──── + ────
 2      2

Integration with Limits

A slightly more complex use case of the integral() function, is when we need to apply limits. Here’s an example that was shown in the official SymPy docs.

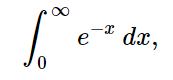
So how do we go about making the integral expression for this? Well, all we need to do is add an extra parameter in the integrate() function, which define the upper and lower limit.

integrate(exp(-x), (x, 0, oo))

The exp() function represents the “e”, which can be found in the SymPy library. The oo that you see as the upper limit is actually two o’s (the letter o) used to represent infinity in SymPy.

More information about limits in SymPy can be found by following this link.

Derivative and Integral

What if you didn’t want the differentiated equation, rather you wanted a “representation” of it instead. Not sure what that means? Let me show you.

SymPy has the ability to represent expressions “Symbolically”, so it can represent a differentiated equation in the following manner.

from sympy import symbols, Derivative
x, y = symbols("x y")

expr = x**2 - x - 6

print(Derivative(expr, x))

Derivative(x**2 - x - 6, x)

Similarly, we can represent Integrals in the following manner.

from sympy import symbols, diff, Integral
x, y = symbols("x y")

expr = x**2 - x - 6

print(Integral(expr, x))

Integral(x**2 - x - 6, x)

You may find a feature like this useful in certain situations, where representing the object as a Derivative is important, rather than evaluating it.

If you want to evaluate a Derivative or Integral expression into the regular differentiation/integration version, then use the doit() method on the object.

This marks the end of the Differentiation and Integration with Python SymPy Tutorial. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can be asked in the comments section below.