In this article, we will be discussing the Python Insertion Sort Algorithm in complete detail. We will start with it’s explanation, followed by a complete solution which is then explained by breaking it down into steps and explaining each of them separately.
At the end we have also included a small comparison of the Python Insertion Sort with others similar algorithms. As a bonus, we also have a video explanation of the Insertion Sort Algorithm, which is included at the very end of the tutorial.
Methodology
The Insertion sort algorithm works off the concept of dividing the array into two parts. The first part is sorted, while the second is not. The first step in any Insertion sort algorithm is to treat the first element in the array, as the first part. Basically you can envision a separating line between the first element, and the rest of the values.
We then begin inserting values from the unsorted part, into the sorted part. We do so by picking the first element of the unsorted part, and pushing it back into the end (after the last element in the sorted part. If the new element is less than the last value in the sorted part, we move it back once more.
We keep moving it like this until the value behind it is greater than the new inserted value. We repeat this process till there are no elements left in the unsorted part.
Solution
Here is a really quick and short solution to the Insertion sort algorithm in Python. We begin the for loop from index 1 (instead of index 0), as we are supposed to ignore the first value in the array.
def insertion_sort(array):
for i in range(1, len(array)):
sort_value = array[i]
while array[i-1] > sort_value and i > 0:
array[i], array[i-1] = array[i-1], array[i]
i = i - 1
return array
A = [4,6,8,3,2,5,7,9,0]
print(insertion_sort(A))
Next up is the while loop, which runs until the next value, (the first value in the unsorted part) has been correctly placed and sorted in the sorted part. Using the Python syntax, we are able to perform a quick swap within a single line, instead of having to use 3.
Explanation
This is the initial array or list of numbers that we will be sorting in this example.
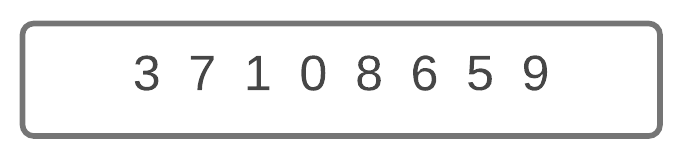
The first step is to begin the for loop from index 1, which is also another way of saying, split the array into two parts like the image below. The first part is index 0, which is known as the sorted part. (This is because is an array contains 1 element, it’s automatically a sorted array).

We will now point the for loop “i” at index 1, where the value “7” resides. We’ll be using an arrow to show the currently selected value at index i.
The currently selected value is the one we will compare against the previous one. Remember, that there are two things to check. The first is whether the value of i is greater than 0, and the second is whether the value at i - 1 is greater than the value at i. If both of these conditions are true, we will swap the i - 1 and i values.
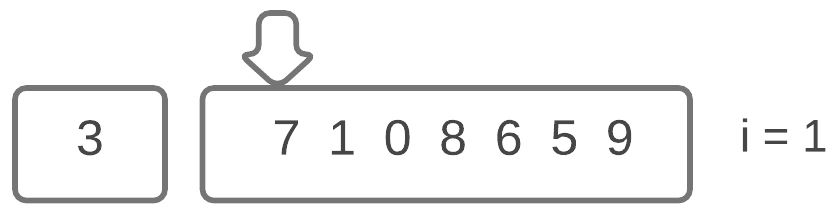
Since 3 is not greater than 7, and i is 1, we will not swap, and instead increment i. We can now assume that 7 is in the sorted part of the array. We have visualized this in the image below.
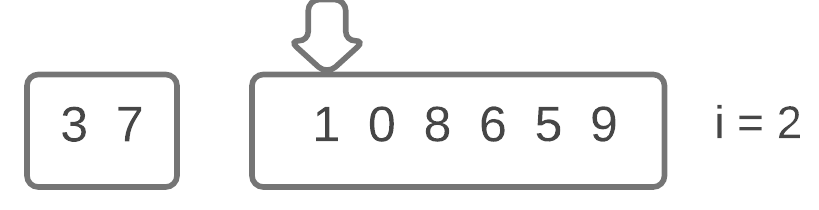
In this second comparison, both conditions have held true, as 7 is greater than one. We will hence swap both of them.

We will still continue, as it is a while loop and will not break until either one of the two conditions returns false. 3 is greater than 1, and i is greater than 0, hence we will swap 1 and 3 as well.

By now you should have gotten the basic gist of how it works. We’ll now speed up a bit.
We now make another pass in the for loop, due to which the value of i is set to 3, causing it to point to the value 0. We will make three swaps in total, until we have set 0 all the way back to the start, at index 0.
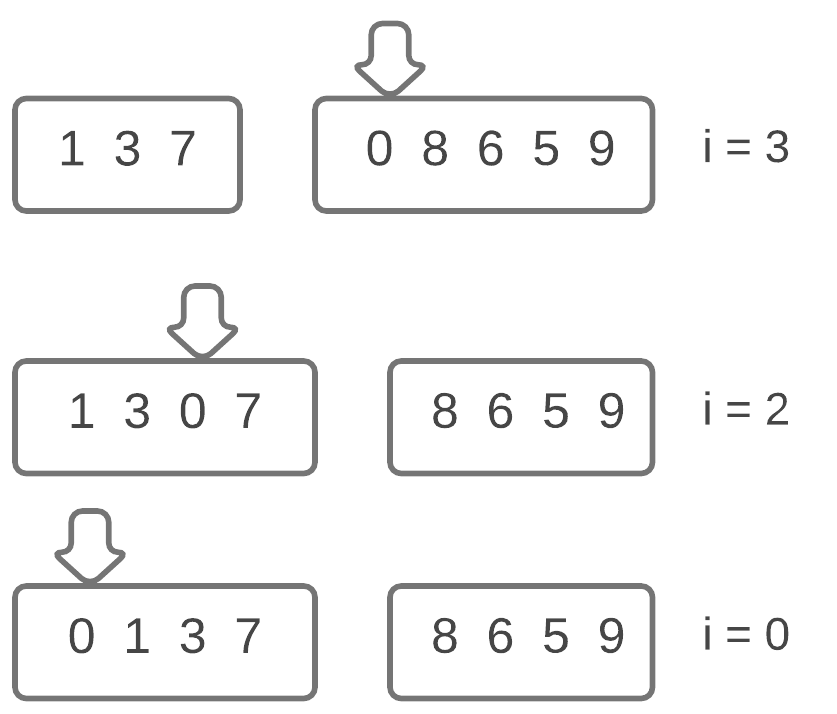
The next value 8, is larger than 7, so we’ll ignore it and move to the next iteration of the for loop, making i = 5.
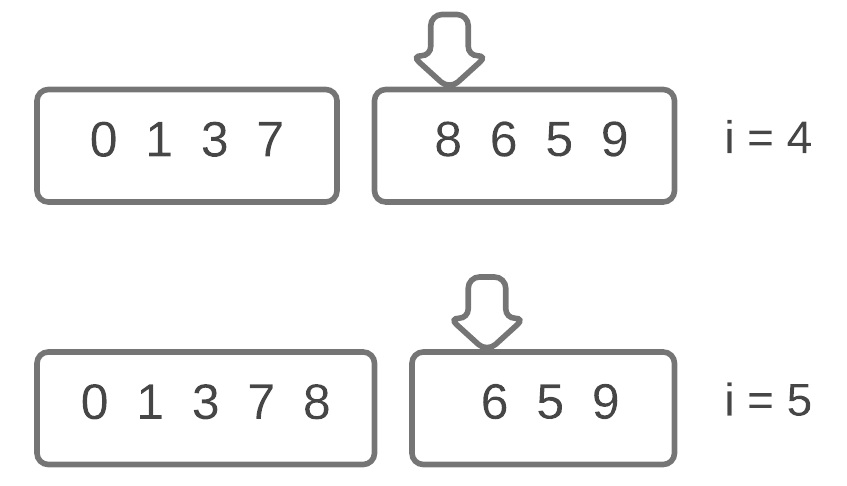
We will swap 8 and 6, and then swap 7 and 6 till it is at it’s correct position. At i = 3, the condition of the i - 1th value being greater than the ith value fails as 3 is not larger than 6. Hence we end the while loop, and proceed to the next iteration of the for loop.
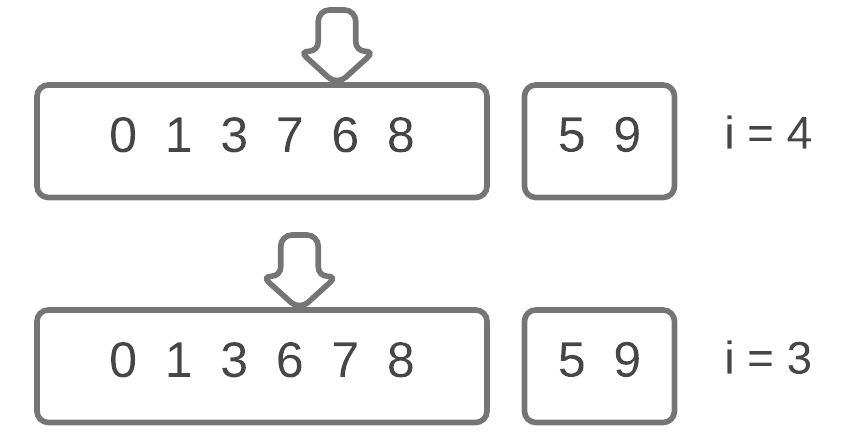
We are now almost done, and are at the 7th iteration of the for loop. Like before, we will swap the value at i = 6 with the i - 1 value till it reaches the correct position. In this case it ends up at i = 3.
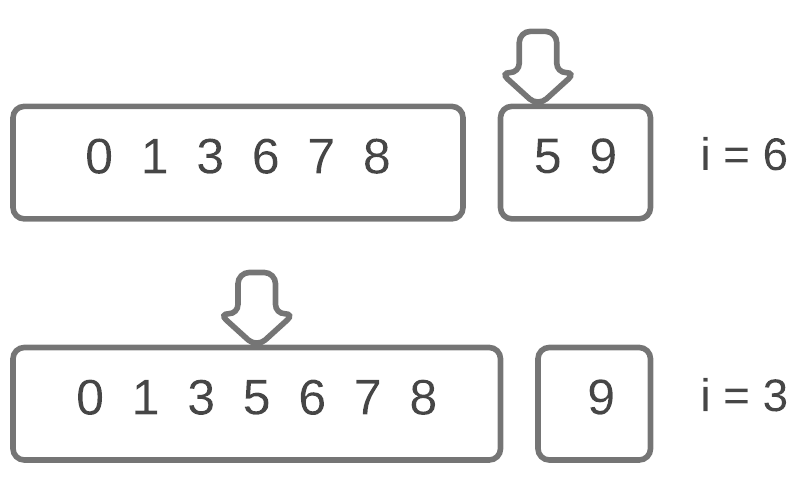
We are now left with just 9, which doesn’t need to be sorted as it’s already in the correct position. (In the language of the algorithm, 8 is smaller than 9, hence the swap doesn’t happen).

Pictured above is the fully sorted array.
Video Tutorial
Here we you can watch the video version of this article. If you are having trouble understanding, or still have some doubts, be sure to check this out. It’s a more interactive experience which will definitely help you.
This marks the end of the Python Insertion Sort Algorithm. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can asked in the comments section below.

😲😲 First well explained and visualized example under the insertion sort.