In this article, we will be discussing the Python Radix Sort Algorithm in complete detail. We will start with it’s explanation, followed by a complete solution which is then explained by breaking it down into steps and explaining each of them separately.
At the end we have also included a small comparison of the Python Radix Sort with others similar algorithms. As a bonus, we also have a video explanation of the Radix Sort Algorithm, which is included at the very end of the tutorial.
Methodology
One interesting thing about Radix Sort is that unlike most the sorting algorithms, it is not comparison based. Meaning, that there are no direct comparisons carried out amongst the values being sorted. Another interesting point is that Radix sort can be used to effectively sort other types of data, besides just numbers, such as strings.
Big O notation: d * (n + b)
n is the number of digits, and b is the base being used (10 for numbers, and 26 for characters). The value of d is logbk, where k is the largest number (such as 845). D is basically influenced by the number of digits in the largest number of the array (such as 3 for 845).
Radix sort can be extremely fast under certain circumstances and is best used when sorting integers. For large lists of numbers, radix sort has a pretty low time complexity and will outperform most other sorting algorithms.
Radix Sort Solution
This is the complete solution to the Radix Sort Algorithm. It’s fast and comparatively easy to understand. We have divided the various tasks required into several functions. In this section we’ll explain the use of each function, and in the next we will explain how Radix Sort works with a worked example.
(Don’t’ give up on understanding it before you read the whole tutorial. The more you read, the more sense it makes. You can also use the video at the bottom, for a more visual explanation).
# get number of digits in largest item
def num_digits(arr):
maxDigit = 0
for num in arr:
maxDigit = max(maxDigit, num)
return len(str(maxDigit))
# flatten into a 1D List
from functools import reduce
def flatten(arr):
return reduce(lambda x, y: x + y, arr)
def radix(arr):
digits = num_digits(arr)
for digit in range(0, digits):
temp = [[] for i in range(10)]
for item in arr:
num = (item // (10 ** digit)) % 10
temp[num].append(item)
arr = flatten(temp)
return arr
array = [55, 45, 3, 289, 213, 1, 288, 53, 2]
array = radix(array)
print(array)
The number of passes Radix Sort makes in total, depends on the highest number of digits in a number in the array of numbers. To find this, we created the function num_digits(), which returns the maximum number of digits in any number of the array.
The flatten() function is another handy function we made to convert 2D arrays into 1D arrays. The technique we used, with the Python Reduce function is just one of the many techniques that you can use. Feel free to use an inbuilt way, or build your own.
Before flatten -> [[20], [21], [922], [3, 53, 73], [384], [], [], [], [8], [89]]
After flatten -> [20, 21, 922, 3, 53, 73, 384, 8, 89]The above output we took from the Radix Sort Algorithm, shows what the flatten() function does. How did it end up as a 2D array in the first place? Read the next section to find out.
Radix Function
Now we are moving onto the main function, the Radix Sort function. This is where the actual logic for the Radix Sort Lies.
def radix(arr):
digits = num_digits(arr)
for digit in range(0, digits):
The first line of the radix() calls the num_digits() function and finds the max number of digits. The second line begins a for loop, that makes a number of passes, equal to the number of max digits.
The next line sets up a 2D array, with the sub-lists in it. We do this with the help of list comprehension. This is just a temporary list that will store values until we can flatten it, and store it within the main array that we passed into the radix() function.
temp = [[] for i in range(10)]
To help you understand, the above line produces the following list if you were to print it out.
[[], [], [], [], [], [], [], [], [], []]We refer to these 10 sub-lists as the 10 buckets, which represent the numbers 0 – 9. If you were sorting strings, there would be 26 buckets for a - z. In this tutorial, we will be sticking to sorting numbers, but the concept remains the same.
It is within these 10 buckets that we will be sorting the values in the array.
Bucket Sorting
This is the Bucket sorting logic of the Radix Sort Algorithm. The for loop here will iterate over the array, element by element and perform an operation on it, to judge it’s position in the 2D array (temp). In other words, to determine which bucket is goes into.
In Radix Sort, we evaluate each number’s digits individually. For the number of 922, we will make three passes in total. On the first and second pass, it will be sorted in the 3rd bucket (first bucket is zero) and on the third pass it will be sorted into the 10th bucket.
for item in arr:
num = (item // (10 ** digit)) % 10
temp[num].append(item)
The above code is incharge of locating the appropriate digit, depending on which pass is currently happening. It’s easy for us to see which buckets 922 should go into, but the above calculation is required for the computer to know this. ( The // operator returns a whole number, after removing the decimal part from the division result).
Let’s take the number 922, and try finding the bucket it’s supposed to go on the second pass. The digit value is 1, ( it was 0 on the first pass, in the first for loop). We thus end up with 922 // 10, which gives us 92. 92 % 10 gives us 2. This means that we will append the number (922) to the 2nd index of temp, which means the third bucket.
After each pass, we will then call the flatten function on the temp array, and assign it back into the main array. The temp array is refreshed each pass of the for loop.
So how does this bucket system sort the array? Look at the below example for that. It may sound strange, but doing this on every number in the array actually sorts it.
Explanation
This is the array on which we will be applying the Python Radix sort algorithm.

Pictured below is the three passes that will take place on the above array. In the first Pass, all the numbers are sorted by the first digits (first from the right). In the second pass, they are sorted by the second digit. (Those numbers without a second digit are assumed to have 0 there). In the third pass, they are sorted by the third digit. As you can see, with each pass the array gets more and more sorted.
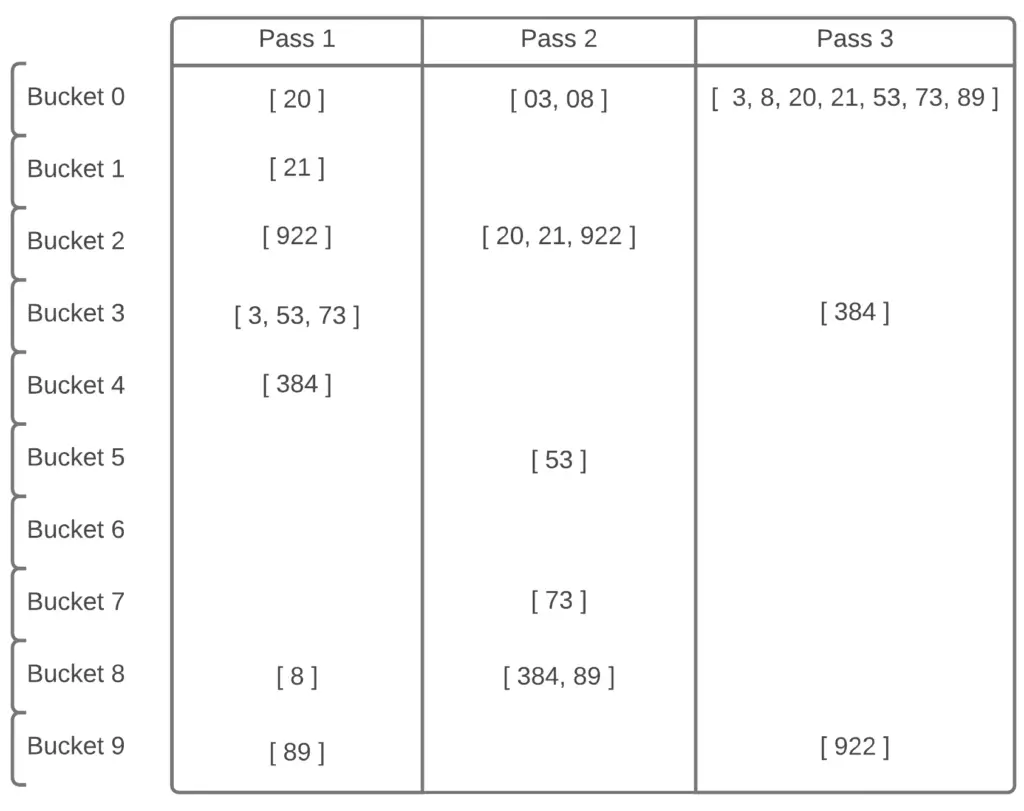
You should now go back and review the logic of the Radix Sort that we explained earlier. In the first section, we just discussed it’s working. In this section, we’ve actually shown it in use.

This is what the main array looks like, after you flatten the temp array and assign it to it, after the first pass. Notice how they are all ordered by the first digits.

This is what the array looks like, after the second pass. Notice how they are all sorted by both the first and second digits now. If you were to remove the two 3-digit numbers, it would be completely sorted.

This is the array after the final pass, showing a completely sorted list of numbers.
Video Tutorial
Here we you can watch the video version of the Python Radix Sort Algorithm. If you are having trouble understanding, or still have some doubts, be sure to check this out. It’s a more interactive experience which will definitely help you.
This marks the end of the Python Radix Sort Algorithm Tutorial. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can be asked in the comments section below.
