In this article, we will be discussing the Python Counting Sort Algorithm in complete detail. We will start with it’s explanation, followed by a complete solution which is then explained by breaking it down into steps and explaining each of them separately.
At the end we have also included a small comparison of the Python Counting Sort with others similar algorithms. As a bonus, we also have a video explanation of the Python Counting Sort Algorithm, which is included at the very end of the article.
Methodology
The Counting Sort Algorithm belongs to the Category of sorting algorithms which do not require comparisons between values. These types of sorts are known as non-comparison based sorts. Instead, the Counting sort uses a rather intriguing and intricate way of correctly judging the positions of each value in the list.
It makes several passes over the list of numbers through out the sorting process. The first pass is required to find the max number in the list. We then use this number to generate a list of size of max number + 1. We then count the number of times instances of each number that appears in the array, and store this count value in the list we just created. After completing the counts array, we iterate over the whole thing, cumulatively summing up all the count values inside it.
Finally, by using a little formula we are able to correctly determine the index of each number, within a newly created array of size n, where n is the number of digits in the original array. This new array, is a fully sorted version of the original array of unsorted numbers.
Counting Sort Algorithm (Code Explanation)
The main body of the explanation was given in the above methodology section. You can cross reference the above explanation with the below code. The comments will help you understand which each part of the counting sort function is doing.
def counting(data):
# Creates 2D list of size max number in the array
counts = [0 for i in range(max(data)+1)]
print(counts)
# Finds the "counts" for each individual number
for value in data:
counts[value] += 1
print(counts)
# Finds the cumulative sum counts
for index in range(1, len(counts)):
counts[index] = counts[index-1] + counts[index]
print(counts)
# Sorting Phase
arr = [0 for loop in range(len(data))]
for value in data:
index = counts[value] - 1
arr[index] = value
counts[value] -= 1
return arr
data = [2, 7, 16, 20, 15, 1, 3, 10]
print(counting(data))
For the full worked example, refer to the section below.
Counting Sort Algorithm – Worked Example
A complete worked example on the Counting Sort Algorithm.

We’ll be using the above list of numbers in our Counting Sort Example.

The first thing we do is to create an empty array as shown above, with all values initialized to 0. In this array, we will be storing the “counts” for each object, and later the sum of counts.

The first number in the array is 8, hence we increment the 8th index by 1.

The second number in the array is 1, hence we increment the 1st index by 1.
We continue on in this manner until we are left the following array.

Notice that 2 and 5 have two occurrences in the list of numbers, hence why they have 2 counts.
Sum Of Counts
We will now begin summing the counts, cumulatively. If you don’t understand this term, just watch the images closely.

We begin summing the values, starting from the 1st index. Check out the for loop in the Counting Sort Algorithm solution, and you’ll notice it also starts from 1, instead of 0. This is because we sum the current index (1) and the index - 1 value. Attempting to access index – 1 at index 0 would lead to an error.

At index 1, basically added 1 + 1. The first one came from index 1 itself, and the other come from index 0.

Over here we added 2 from index 1, and 2 from index 2, resulting in 4.

We continue this process until we’ve summed up all of the values. The final number should be equal to the number of elements in the array.
Sorting the Values

We will now begin placing values from the original array, into a new array of size n, where “n” is the number of elements in the original array. The part of the code we are discussing in this section has been included below.
for value in data:
index = counts[value] - 1
arr[index] = value
counts[value] -= 1
In short, we first locate index by iterating over the original array, and use it’s values as indexes for the count array. After subtracting one from it, we get the correct index of the value in the new array. We then decrement the count in the counts array.

In the image below, the first array represents the sum counts array, and the second represents the new array in which we are sorting.
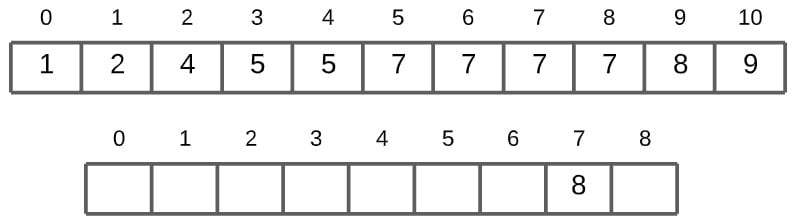
The first value in the data array is 8. At the 8th index of the sum counts array, the value is 8. We will then subtract one from 8, which gives us the correct index of the value in the array. We then store it using the following line of code: arr[index] = value. And finally, we subtract the sum count of 8 by 1, so it’s now 7. This part will make sense later on.
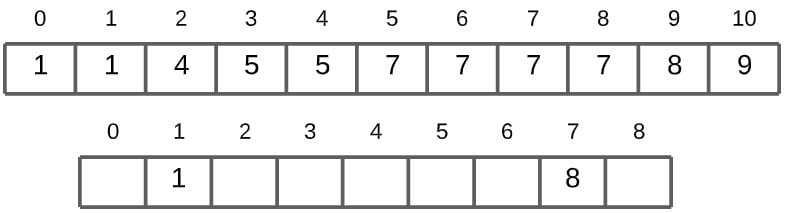
In the next iteration, the same process repeats. The next value is 1. The value at index 1 in sum counts is 2. 2 – 1, gives us two as the correct index. We then store 1 at that index in the array.
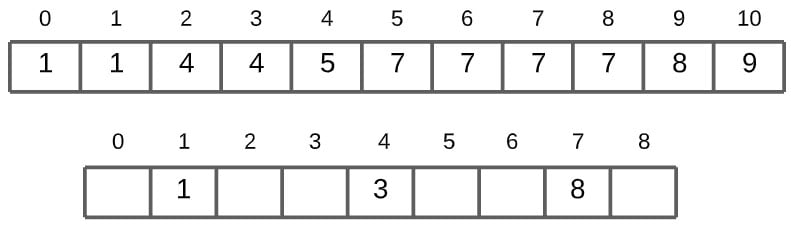
Next iteration we get the value 3. The value at index 3 in the sum counts array is 5. Subtracting 1 from it gives us 4, which is the index of the array, where we assign the value 3. And as before, we decrement the count value of three, from 5 -> 4.
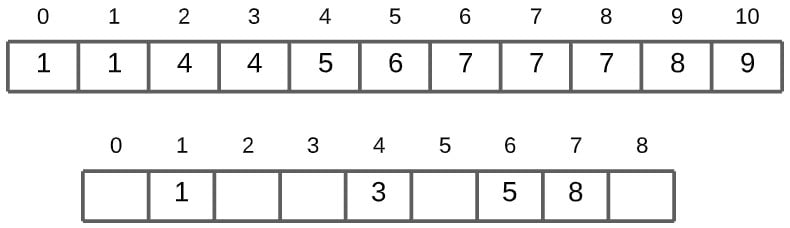
The next value is 5. There are actually two 5’s in this array. So how will Counting Sort Algorithm determine the correct positions for both? Well, that’s why we subtract one from the index. You’ll understand this when 5 next appears. For now, we just stored it at the index 6, after applying the formula.
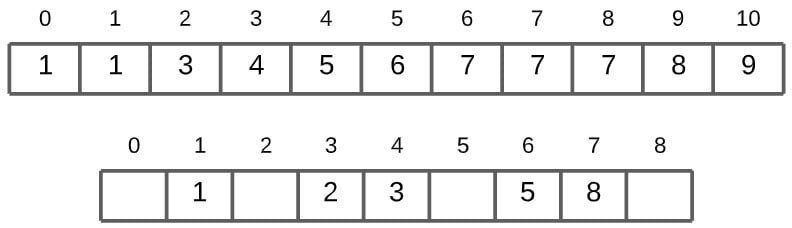
Next is value 2. Same scenario as 5, as it has another repeated value that will show up later. For now though, we just locate it’s correct index 3, and then decrement the sum count from 4 -> 3.
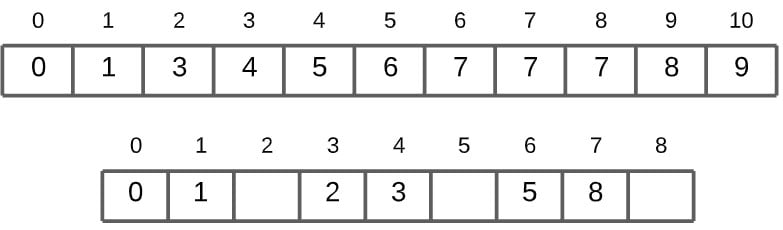
Next value 0, is stored at index 0.
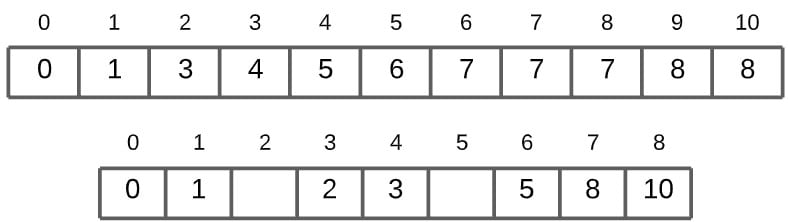
The next value 10, is stored at index 8.
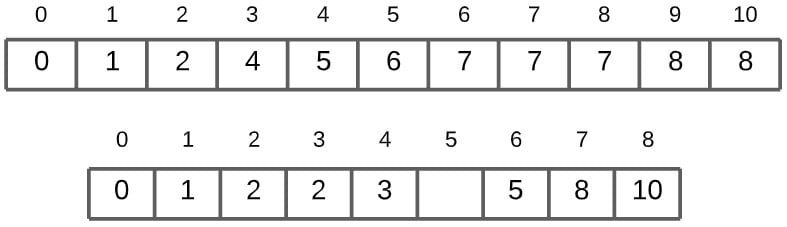
We now have our repeated value, 2. If we had not decremented the sum counts, we would have gotten the same index 3, which is the index of an already occupied slot by the same value (2). Due to the decrement though, it now points to the open slot right before it, index 2.
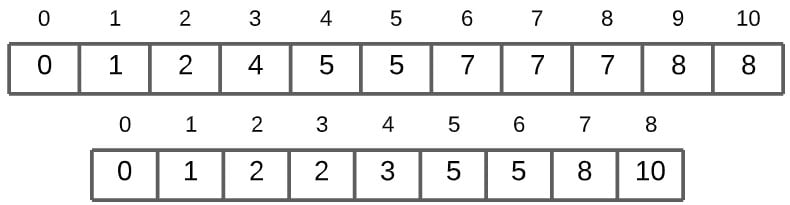
We do the same with 5. counts[5] is 6, from which we subtract 1. We get 5, and we store the value 5 at index 5 in the array. Finally we subtract 1 from the counts array, leaving us with 5.
In short, the reason we decrement is simply to account for the repeated values.
Video Tutorial
Here we you can watch the video version of the Python Counting Sort Algorithm. If you are having trouble understanding, or still have some doubts, be sure to check this out. It’s a more interactive experience which will definitely help you.
This marks the end of the Python Counting Sort Algorithm Tutorial. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can be asked in the comments section below.

This doesn’t work for negative cases.