In this article, we will be discussing the Python Merge Sort Algorithm in complete detail. We will start with it’s explanation, followed by a complete solution which is then explained by breaking it down into steps and explaining each of them separately.
At the end we have also included a small comparison of the Python MergeSort with others similar algorithms. As a bonus, we also have a video explanation of the Merge Sort Algorithm, which is included at the very end of the article.
Methodology
A rather unique type of sort which breaks a list into two (or accepts two lists) and begins merging them element by element, in a sort manner. The end result is a new array, which contains the elements of both lists in a sort manner.
Despite being more stable than sorts like quicksort (better in worst case scenarios), Merge sort uses more memory as it needs to create a new array/list for the final values. (It doesn’t sort in place)
Big O notation = n * log(n) (Average Case)
Merge Sort Algorithm
Here is our solution to the Merge Sort Algorithm in Python. A full explanation for this code is included in the next section.
def mergesort(x):
if len(x) < 2: # Return if array was reduced to size 1
return x
result = [] # Array in which sorted values will be inserted
mid = int(len(x) / 2)
y = mergesort(x[:mid]) # 1st half of array
z = mergesort(x[mid:]) # 2nd half of array
i = 0
j = 0
while i < len(y) and j < len(z): # Stop if either half reaches its end
if y[i] > z[j]:
result.append(z[j])
j += 1
else:
result.append(y[i])
i += 1
result += y[i:] # Add left over elements
result += z[j:] # Add left over elements
return result
Code Explanation
Below is an image that is meant to represent the Python Merge sort Algorithm.
Before proceeding to the explanation, please spend a few minutes trying to follow the steps in the image below yourself, with reference to the above python merge sort algorithm.
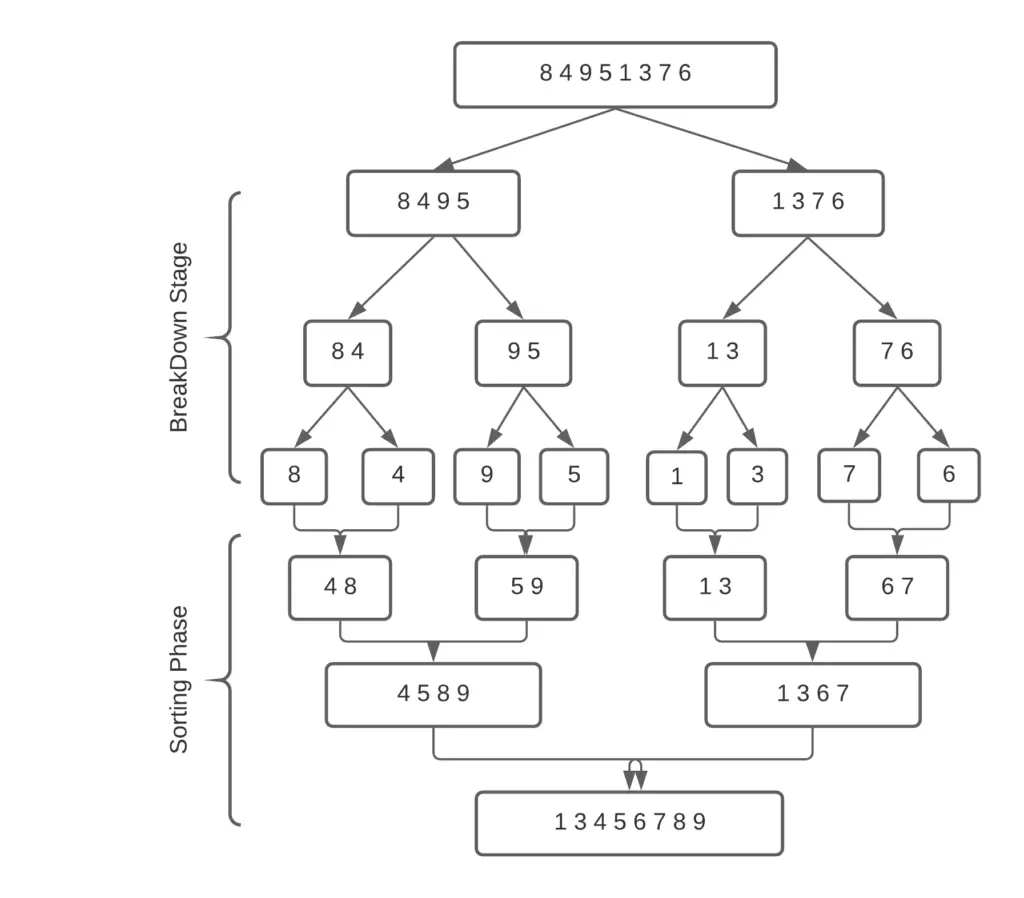
I have divided the explanation of the Merge sort algorithm into two, for the sake of explanation and understanding.
Breakdown Stage
The breakdown stage is still line 9, in the above code. Basically until all the recursive calls have been made, right down to the last element, the program will not proceed any further. This is further reflected in the above image.
y = mergesort(x[:mid]) # 1st half of array
z = mergesort(x[mid:]) # 2nd half of array
So how exactly are these recursive calls being created, and what effect do they have? Well, as you can see in the snippet above, we make two recursive calls, one on each half the array. And if you take a look at line 2 in the code (in the main solution) , you can see that we have a condition that checks the size of the array, and begins returning if length is down to one single value.
Now if you take a good look at the diagram, you’ll see that half way through we are left with individual values. In the sorting stage, we will begin putting together all these values in a sorted manner into a new array called result.
Sorting Stage
This brings us to the sorting stage, The while loop here is completely responsible for this. As you can see, the while loop will run as long as either list hasn’t reached it’s end. We’ll take care of leftover values later.
while i < len(y) and j < len(z): # Stop if either half reaches its end
if y[i] > z[j]:
result.append(z[j])
j += 1
else:
result.append(y[i])
i += 1
The if statement determines which value will be appended to the result array. Since i and j are both initialized with 0, the first check will be between the first two elements. If the first element of the first half is smaller, then it will be added either the first element of the second list is added.
Once we do this, we increment the i or j counter, (depending on which value was added). This indicates that we should now be pointing to the next value. For example, if the first element of the y array was picked (first half), then we will increment i by 1. So the next comparision will be between y[1] and z[0].
result += y[i:] # Add left over elements
result += z[j:] # Add left over elements
return result
This will continue until either list has reached it’s end, after which we add in any left over values, and return the final array.
Video Tutorial
Here we you can watch the video version of this article. If you are having trouble understanding, or still have some doubts, be sure to check this out. It’s a more interactive experience which will definitely help you.
This marks the end of the Python Merge Sort Algorithm. Any suggestions or contributions for CodersLegacy are more than welcome. Questions regarding the tutorial content can be asked in the comments section below.
