In this tutorial we will discuss the Topological Sort Algorithm, complete with it’s code in C++.
While the Topological Sort Algorithm is technically a sorting algorithm, it is not actually used in the same way as other sorts like Quicksort and Merge Sort. Topological Sorting is actually used to sort “Dependencies”, or in simpler terms, “The order in which items depend on each other”. This will make more sense once we get to the Diagrams and the Code.
Another rather interesting thing about Topological Sort, is that there is not a “unique” solution, which means that multiple answers to one problem set may exist.
Intuition on Topological Sort
Before we proceed, we will try to develop your understanding of topological sort, and what “dependencies” are.
We say that Action A, depends on Action B, if Action A requires Action B to be carried out first, before it can be executed. In real-life situations, we see many such examples of such things, for example, “Driving a Car”, has many dependencies such as “Having a Valid License” and “Owning a Car”.
The job of Topological Sort is to sort a list of items/actions in such a way, that the dependencies for an item, always appear after it in the list. So if we were to sort the following list, where:
- Action A -> Driving a Car
- Action B -> Having a Valid License
- Action C -> Owning a Car
Then the answer would be either A, B, C or A, C, B, where A depends on B and C. This is because neither B or C depend on each other, so swapping their positions does not result in an incorrect answer.
Topological Sort – Dependency Diagram
On to the actual Tutorial on Topological Sort.
Below we have the graph with which we will be working in further examples. We have a total of 7 Nodes or “Items”, which each depend or relate to each other in some unique way.
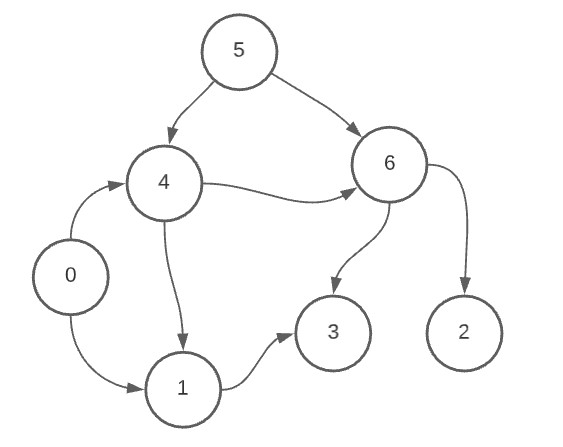
We can observe for example, that Node 5 depends on both 4 and 6. But no Node depends on node 5. On the other hand, Node 4 depends on 1 and 6, but is also a dependency for Node 5 and 0.
Such a situation is rather tricky to resolve dependencies for, which is why we use the Topological Sort Algorithm which can do this for us.
Topological Graph Code
Here is the complete code. The step-by-step explanation can be found in the next section. The output is also discussed in detail towards the end of the tutorial.
#include <iostream>
#include <list>
#include <stack>
#include <vector>
using namespace std;
class Edge {
public:
Edge *head, *tail;
Edge() {
head = nullptr;
tail = nullptr;
}
};
class TopologicalSort {
public:
TopologicalSort(int size) {
this->size = size;
adj.resize(size);
visited = new bool[size];
}
void topsort() {
for (int i = 0; i < size; i++)
visited[i] = false;
for (int i = 0; i < size; i++) {
if (visited[i] == false) {
dfs(i);
}
}
display();
}
void dfs(int i) {
visited[i] = true;
for (int j = 0; j < adj[i].size(); j++) {
int node = adj[i][j];
if (visited[node] == false) {
dfs(node);
}
}
stack.push(i);
}
void addEdge(int tail, int head) {
adj[tail].push_back(head);
size = adj.size();
}
void display() {
if (stack.empty()) return;
for(int i = 0; i < adj.size(); i++) {
cout << stack.top() << " ";
stack.pop();
}
}
~TopologicalSort() {
delete[] visited;
}
private:
bool *visited;
vector<vector<int> > adj;
stack<int> stack;
int size;
};
int main() {
TopologicalSort tsort(7);
tsort.addEdge(5, 6);
tsort.addEdge(5, 4);
tsort.addEdge(4, 1);
tsort.addEdge(4, 6);
tsort.addEdge(0, 4);
tsort.addEdge(0, 1);
tsort.addEdge(1, 3);
tsort.addEdge(6, 3);
tsort.addEdge(6, 2);
tsort.topsort();
}
Code Explanation
Here is a complete explanation for the code, which we have separated into small blocks which we will address separately.
class Edge {
public:
Edge *head, *tail;
Edge() {
head = nullptr;
tail = nullptr;
}
};
Here we have made our “Edge” class. We needed something to keep track of the connection between two “Nodes” or “Elements”. Hence we created the Edge class, which has two pointers in it.
The head represents the value to which the arrow is pointing, and the tail is the value from which the arrow is extending. For e.g: If you look at the previous graph we made, the edge for the Nodes 5 and 6, have “head” pointing to 6, and tail pointing to 5.
Topological Sort Class
class TopologicalSort {
public:
TopologicalSort(int size) {
this->size = size;
adj.resize(size);
visited = new bool[size];
}
~TopologicalSort() {
delete[] visited;
}
private:
bool *visited;
vector<vector<int> > adj;
stack<int> stack;
int size;
};
This here is the Topological Sort Class. It has 4 member variables declared in private.
1.A pointer which we allocate some memory in the constructor, called visited. This pointer points to an array of type bool, of size n where n is the number of nodes. This basically tracks which nodes have been visited, and which have not. This is important because we don’t want to visit the same node twice. For e.g, if the third node has been visited, the second index of the visited array will have the value true.
2. This is the adjacency matrix, which stores information regarding the edges and Nodes. If there are10 nodes, then there are 10 vectors within the adjacency matrix. Each vector stores integers, used to indicate which Nodes the Node is pointing to. For example, Vector 1 represents Node 1. If Node 1 has two edges leading to Node 3 & 5, then we will push the integers 3 & 5 into Vector 1 to symbolize this relationship.
3. This is a stack, which we will use throughout the sorting process.
4. The size, which is basically just the number of nodes/elements.
Adding Edges
void addEdge(int tail, int head) {
adj[tail].push_back(head);
size = adj.size();
}
Here’s a function that’s part of the Topological Sort Class. We’ll be using this to add new edges into our topological graph. We need two pieces of information to do so. The Node from which the arrow is originating (tail), and the Node to which the arrow is pointing (head).
We then store this information in the adjacency vector.
Topological Sort
This is the driver function for the topological sort algorithm. It involves the use of two for loops. The first iterates over the whole visited array, and initializes all values to false.
The second, iterates over every Node that has not been visited yet, and performs Depth First Search on it,
void topsort() {
for (int i = 0; i < size; i++) # Initialize visited array to false
visited[i] = false;
for (int i = 0; i < size; i++) { # Perform DFS on all unvisited nodes
if (visited[i] == false) {
dfs(i);
}
}
display();
}
Depth-First Search
This function performs a Depth-First Search on a specific node. You can think of this as a form of traversing the graph.
Let’s refer to the Node we are performing D.F.S on, as the “Root Node”. We first need to find the Nodes to which the Root Node is connected/dependent on. This can be done by checking the adjacency matrix. We will then proceed to iterate over it’s adjacency vector and recursively perform D.F.S on any Nodes that haven’t been visited yet.
void dfs(int i) {
visited[i] = true;
for (int j = 0; j < adj[i].size(); j++) {
int node = adj[i][j];
if (visited[node] == false) {
dfs(node);
}
}
stack.push(i);
}
A node is marked as visited whenever the D.F.S function is called on it. This is done at the start of the function.
Final Output
Here is the final output that we would get, if we ran the full code using the data provided to us.
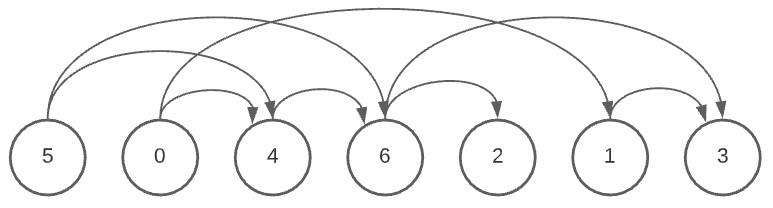
If you examine it carefully, you will notice that there is a pattern to the direction of the arrows. All of the arrows point towards the right-hand side. This is also a means of verifying that our answer is correct. We can now say that the dependencies have been sorted correctly.
In other words, the purpose of topological sort is to return an array of the nodes where each node appears before all the nodes it points to.
This marks the end of the Topological Sort Algorithm Tutorial. Any suggestions or contributions for CodersLegacy are more than welcome. Question regarding the article content can be asked in the comments section below.
